információs technológia
Lebegőpontos ábrázolás
Számrendszerek alapjai
Lebegőpontos ábrázolás
Lebegőpontos számrendszerek alapjai
- Nagyobb pontosság vs. több paraméter tárolása: A lebegőpontos számábrázolás lehetővé teszi nagyon nagy vagy kicsi számok ábrázolását, de cserébe bonyolultabb a számítási folyamat és több paramétert kell tárolni.
- 7 paraméter definiálja a rendszert:
- Számrendszer alapja (rb).
- Előjel nagysága
- Mantissza (M) alapja és nagysága
- Kitevő alapja (re)
- előjel és hosszúság
Egyszerű matematikai jelölés:
Felhasználás: például a proton tömege (1.673 x 10^-24)
Mantissza igazítása: a számot úgy kell alakítani, hogy a mantissza [1/rb, 1] intervallumba essen. Példa: 32768 -> 0.32768 x 10^5
Az eredeti számot normálizáljuk és a kitevőt hozzáigazítjuk.
Lebegőpontos rendszer paraméterei
Mantissza értéke (VM)
Maximális érték:
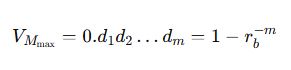
Minimális értéke
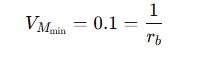
d1, d2, …, dm a mantissza számjegyei
rb a számrendszer alapja (pl bináris számrendszer esetén rb=2)
a mantissza értéke a [1/rb, 1) intervallumba esik, tehát 1/rb ≤ VM < 1
A mantissza legkisebb lehetséges értéke: 1/rb. Ez akkor következik be, ha a mantisszában csak egyetlen 1 szerepel az első helyiértékben és minden további helyiérték 0.
A mantissza legnagyobb lehetséges értéke: 1 (de nem éri el, csak megközelíti) Ez akkor következik be, ha az összes helyiérték maximális értékű (bináris esetén mindegyik 1) Ez az intervallum biztosítja, hogy a számot mindig normálalakban fejezzük ki, azaz a legnagyobb helyiértékű számjegy (az első számjegy) mindig 1 legyen, és ezzel az ábrázolás hatékonyabbá válik.
Példák különböző számrendszerekben:
1. Bináris rendszer (rb=2)
A mantissza intervalluma: [1/2,1) = [0.5, 1), példa: 0.111 = 0,5+0,25+0125 = 0,875
2. Tízes számrendszer (rb=10)
A mantissza intervalluma: [1/10,1) = [0.1, 1), példa: 0.999
rb^-m
az alap reciprokát (1/rb)-t az m-edik hatványra emeljük. Ez az érték a mantissza legkisebb helyiértékének értékét adja meg. Az exponens (-m) határozza meg, hogy a számjegy milyen távol van a tizedespontottól.
Példa: rb=2. Tegyük fel, hogy a mantissza m=3. Az rb^m =2^-3= 1/2^3=0.125.
A mantissza legkisebb helyiértékének értéke 0.125
FPN jellemző paraméterei (V – Value, FPN . Floating Point Number):
1. Számrendszer és kitevő alapja (rb, re)
rb: a számrendszer alapja (pl. 2-es, 10-es)
re: a kitevő alapja, általában megegyezik rb-vel. Példa: IEEE-754 szabványban rb =re =2, mert bináris lebegőpontos ábrázolást használunk.
A mantissza értéke: a mantissza a szám tényleges értékének [1,rb) közötti részét tartalmazza. Maximális érték: VMmax: 1-rb^-m, ahol m a mantissza bitjeinek hossza.
Minimális érték: VMmin = 1/rb
Radix pont helye (p): meghatározza a mantisszában, hogy hol kezdődik az egész és a tört rész. Normalizált lebegőpontos szám esetén a radix pont mindig a legjelentősebb számjegy után helyezkedik el. Példa: 1.101 x 2^3. A radix pont az 1 után van.
Exponens értékei (VE): a maximális és minimális exponens a szám nagyságrendjének határát jelöli.
Maximális exponens (VEmax): a legnagyobb érték, amit az exponens felvehet. Ez határozza meg, hogy a lebegőpontos szám milyen nagy lehet. Ha például az exponens 8 biten van tárolva (az IEEE-754 szabvány szerint) és excess-127 kódolást használunk:
VEmax=127
Minimális exponens (VEmin): az a legkisebb érték, amit az exponens vehet fel. Ez határozza meg, hogy a lebegőpontos szám milyen kicsi lehet (a legnagyobb negatív kitevővel). Példa, ha az exponens 8 biten van tárolva: VEmin=-126
Lebegőpontos szám értéke (VFPN):
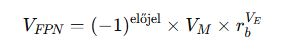
Előjel: (-1)^előjel: meghatározza, hogy a szám pozitív vagy negatív.
0: pozitív
1: negatív
VM: a szám pontos értékének a [1, rb) közötti része
VE: a szám nagyságrendje
Példa: egy szám, amelynek:
mantissza: 1.1101
exponens: VE = 3
számrendszer alapja: rb = 2
előjel: 0
értéke: VFPN = 1.1101 x 2^3 = 1110.1 =14.5
Feladatok
1. Feladat: egy szám mantisszája 1.0110, az exponens: 2, a számrendszer alapja: rb=2 és az előjel: 1. Számold ki a lebegőpontos szám értékét.
Megoldás:
1. lépés: előjel meghatározása. Az előjel 1, tehát negatív lesz. (-1)^1 = -1
2. lépés: mantissza értelmezése:
Az egész rész: 1
Tört rész binárisan: 0110, decimálisan: 0.375
A teljes mantissza értéke: 1.375
3. lépés: kitevő, exponens hatása: rb = 2, tehát 4
4. lépés: a szám végső értéke: VFPN =(-1)^1×1,375×4 = -5,5
2. feladat:
Adott egy másik lebegőpontos szám:
- Mantissza: 1.1011
- Exponens (VE): -1
- Számrendszer alapja (rb): 2
- Előjel: 0 (pozitív)
Feladat: Határozd meg a szám értékét lépésről lépésre! (megoldás: 0,84375)
3. feladat
A következő lebegőpontos szám paraméterei adottak:
- Mantissza: 1.0001
- Exponens (VE): 4
- Számrendszer alapja (rb): 2
- Előjel: 0 (pozitív)
Feladat: Számítsd ki a szám értékét, és ellenőrizd, hogy a végeredmény helyes-e! (megoldás: 17)
4. feladat
Egy lebegőpontos számot a következő adatokkal adunk meg:
- Mantissza: 1.1111
- Exponens (VE): -3
- Számrendszer alapja (rb): 2
- Előjel: 1 (negatív)
Feladat: Add meg a szám pontos értékét normálalakban, majd decimálisan! (megoldás: -0,2421875)
5. feladat
Töltsd ki az alábbi táblázatot:
| Mantissza | Exponens (VE) | Számrendszer alapja (rb) | Előjel (0: pozitív, 1: negatív) | Érték |
|---|---|---|---|---|
| 1.0101 | 3 | 2 | 0 | ? |
| 1.1000 | -2 | 2 | 1 | ? |
| 1.0011 | 1 | 2 | 0 | ? |
| 1.1110 | -1 | 2 | 1 | ? |
Feladat: Számítsd ki az értékeket mindegyik sorra! (megoldás: 10.5, -0.375, 2.375, -0.9375)
