Az IEEE 754 szabvány szerinti -13.75 lebegőpontos ábrázolás részletes bemutatása

A feladat a -13.75 decimális szám 32-bites lebegőpontos formátumban történő ábrázolása az IEEE 754 szabvány alapján.

m=p=24: Mantissza (M): a mantissza 24 biten kerül tárolásra, ami a szám bináris normálalakjának 1 utáni része. A normálalak implicit tartalmaz egy 1. részt, így az ábrázolt mantissza mindig 1.xxxxxx-ként van tárolva
e=8: kitevő. A kitevő 8 biten kerül tárolásra. Az Excess-128 kódolás biztosítja, hogy minden kitevő pozitívként legyen tárolva. 
rb=re=2: alap. Rb és re az alap a lebegőpontos ábrázolásban:
re: a kitevőhoz használt alap, azaz 2^e
rb: a számrendszer alapba (bináris rendszer esetén 2)

1. Mi az a 32-bites lebegőpontos rendszer?

Az IEEE 754 szabvány 32-bitben három részt határoz meg:

1. Előjel (S): 1 bit. Jelöli, hogy a szám pozitív (0) vagy negatív (1).
2. Kitevő (E): 8 bit. Meghatározza a szám helyzetét a normálalakban.
3. Mantissza (M): 23 bit. A szám pontos bináris értékét adja a normálalak törtrészeként.

2. Lépések a -13.75 ábrázolásához

Előjel (S):

– a szám negatív, ezért az előjel bitje = 1

A szám bináris formája

1. Egész rész átváltása binárisra:

13/2 =6 (maradt az 1)
6/2 = 3 (maradt a 0)
3/2 = 1 (maradt az 1)
1/2 = 0 (maradt az 1)
A maradékok fordított sorrendben: 1101

Ellenőrzés: 1102 = 1×2^3  + 1×2^2 + 0x2^1 + 1×2^0 = 8+4+0+1 = 13

2. Törtrész átváltása binárisra:

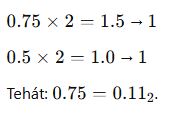
A törtrész binárisra váltásához az alábbi módszert használjuk:

• Szorozzuk meg a törtrészt 2-vel.
• Jegyezzük fel az egész részt (0 vagy 1).
• Ismételjük addig, amíg a törtrész 0 lesz, vagy elérjük a szükséges pontosságot.
  Ellenőrzés: 1x 2^-1 + 1×2^-2 = 0,5+0,25 = 0,75

3. A teljes bináris szám: 

3. Normálalakra hozás

A bináris számot normálalakba írjuk. A normálalak lényege, hogy a számot úgy alakítjuk át, hogy az egész rész mindig 1 legyen, és ezt egy 2^e kitevővel korrigáljuk. Ez a lebegőpontos ábrázolás alapja. 

A számot úgy alakítjuk át, hogy:

• Az egész rész 1 legyen (az 1 az egész szám első számjegye).
• Az összes többi számjegy (egész és törtrész) a törtrészbe kerül.
  Az átalakítást a 2^e kitevővel korrigáljuk, amely megadja, hogy hányszor kell eltolni a tizedespontot balra vagy jobbra. 

Az 1101.11 számot addig toljuk balra, amíg az első számjegy 1 nem lesz. 
Az eredeti bináris szám: 1101.11
A tizedespont 3 helyet mozdult balra: 1,10111
A kitevő ezért: e=3

Az átalakított szám normálalakban: 1101.11=1.10111×2^3

4. Mantissza (M)

 A mantissza a normálalakban szereplő szám törtrésze (az 1 után következő számjegyek). Az 1-et nem tároljuk, mert implicit része a lebegőpontos formátumnak.
A mantissza binárisan: 
M = 10111

Ellenőrzés: 1.10111×2^3 = 1101.11

Az 1.10111 binárisan 1+0,5+0,125+0,0625 = 1,6875. Ezt megszorozzuk 2^3-mal: 1,6875*8=13.75

5. Kitevő (E) Excess-128 kódolással

1. valódi kitevő: e=3
2. Excess-128 kitevő: E=e+128 = 3+128 = 131
3. Binárisan: 131(10) = 10000011(2)

6. Bitmintázat összehasonlítása

Az IEEE 754 formátum szerinti bitmintázat: S | E | M

S=1 (negatív szám)
E=10000011 (kitevő Excess-128 kódolásban)
M=10111000000000000000000 (mantissza 23 biten)

Végső bitmintázat: 1 100000 11 10111000000000000000000

Ellenőrzés: 
S = 1 => negatív szám
E = 10000011(2) = 131. Excess-128-ból való kivonás: e=E128 = 131-128 = 3
M = 10111000000000000000000 hozzáadjuk az implicit 1-et: 1.10111
Normálalak: 1.10111×2^3  binárisan: 1101.11
Visszaalakítva decimálisra: 
Egész rész: 1101 = 13
Törtrész: 0.11 = 0,75 
Összeg: -13.75