Hatvány (elmélet)

Definíció: a hatványozás egy olyan művelet, amely egy számot (az alapot) többször megszoroz önmagával. Az általános alak:

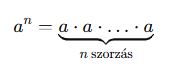
a^a: a hatvány alapja
n: a kitevő 

Szabályok:

1. szorzás azonos alapú hatványokkal: 
a^m x a^n = a^m+n           Példa: 2^3 x 2^4 = 2^3+4 = 2^7

2. Osztás azonos alapú hatványokkal:
a^m : a^n = a^m-n (m>n)  Példa: 5^4 : 5^2 = 5^4-2 = 5^2

3. Hatvány hatványozása:
(a^m)^n = a^mn                 Példa: (3^2)^3 = 3^2×3 = 3^6

4. Szorzat hatványozása
(a x b)^n = a^n x b^n         Példa: (2 x 3)^2 = 2^2 x 3^2 = 4×9 =36

5. Tört hatványozása
(a/b)^n = a^n / b^n            Példa: (2/3)^2 = 2^2/3^2=4/9

6. Nulladik hatvány
a^0 = 1 (a nem lehet nulla) Példa: 10^0 = 1

7. Negatív kitevő
a^-n = 1/a^n                         Példa: 2^-3 = 1/2^3 = 1/8

8. Törtkitevő (gyökvonás)
a^m/n = n√ a^m                  Példa: 8^2/3 = 3√ 8^2 = 3√ 64 =4